How to compute the rotated polygon's coordinates?

CesiumJS
1

Hi All,

I want to rotate a polygon based on the center point using the value of heading, pitch and roll and get the coordinates of each vertex of the rotated polygon, then use these coordinates to do some other calculations for my application.

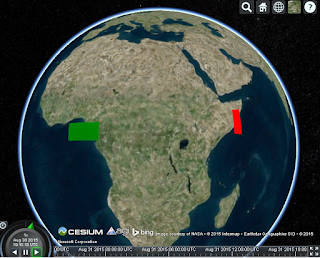
I was trying to compute these coordinates by using a transformation matrix to multiply by the the vertexes of the polygon, respectively, before rotated. To create this transformation matrix, I used Cesium.Transforms.headingPitchRollToFixedFrame. However, the result is not what I expected, even without any rotation, the rotated polygon(red) is away from the original one(green) and seems to be rotated by 90 degree.

I tried to used other methods but still have the same problem.

Does anyone can tell me what I am supposed to do?

Many thanks,

Wei

var viewer = new Cesium.Viewer(‘cesiumContainer’);

var entities = viewer.entities;

var center = Cesium.Cartesian3.fromDegrees(5, 2.5);// The center of the polygon

var heading = Cesium.Math.toRadians(30);

var pitch = Cesium.Math.toRadians(0);

var roll = Cesium.Math.toRadians(0);

// create the transformation matrix based on a specific value of heading, pitch and roll

var rotation = Cesium.Transforms.headingPitchRollToFixedFrame(center, heading, pitch, roll);

// add the polygon without any rotation
entities.add({

polygon: {

hierarchy: new Cesium.PolygonHierarchy(Cesium.Cartesian3.fromDegreesArray([0, 0,

10, 0,

10, 5,

0, 5])),

material: Cesium.Color.GREEN

}

});

// compute the coordinates of each vertex of the rotated polygon

var p1 = new Cesium.Cartesian3.fromDegrees(0, 0);

Cesium.Matrix4.multiplyByPoint(rotation,p1,p1);

var a1 = Cesium.Ellipsoid.WGS84.cartesianToCartographic(p1);

var p2 = new Cesium.Cartesian3.fromDegrees(10, 0);

Cesium.Matrix4.multiplyByPoint(rotation,p2,p2);

var a2 = Cesium.Ellipsoid.WGS84.cartesianToCartographic(p2);

var p3 = new Cesium.Cartesian3.fromDegrees(10, 5);

Cesium.Matrix4.multiplyByPoint(rotation,p3,p3);

var a3 = Cesium.Ellipsoid.WGS84.cartesianToCartographic(p3);

var p4 = new Cesium.Cartesian3.fromDegrees(0, 5);

Cesium.Matrix4.multiplyByPoint(rotation,p4,p4);

var a4 = Cesium.Ellipsoid.WGS84.cartesianToCartographic(p4);

// add the rotated polygon

entities.add({

polygon: {

hierarchy: new Cesium.PolygonHierarchy(Cesium.Cartesian3.fromDegreesArray([

Cesium.Math.toDegrees(a1.longitude), Cesium.Math.toDegrees(a1.latitude),

Cesium.Math.toDegrees(a2.longitude), Cesium.Math.toDegrees(a2.latitude),

Cesium.Math.toDegrees(a3.longitude), Cesium.Math.toDegrees(a3.latitude),

Cesium.Math.toDegrees(a4.longitude), Cesium.Math.toDegrees(a4.latitude)])),

material: Cesium.Color.RED

}

});

viewer.zoomTo(viewer.entities);

``

``

2

You have reference frame problems. This transform takes coordinates in a local reference frame, applies heading/pitch/roll, then projects it into the earth fixed reference frame at the origin (center) position provided. You’ll need to define your rectangle points in a local reference frame before applying this kind of transform. Right now, the rectangle points are in the earth fixed reference frame, with the origin at the center of the globe. You need to project the rectangle points such the origin is at the center of the rectangle.

-Hannah

3

Thank you very much Hannah. It works now.

4

Hi Wei/Hannah,

Could you please provide me sample piece of code to compute rotated polygon coordinates?

Thanks,
Gowtham.

5

Hi Hannah,

If my understanding is correct, after this step “var p1 = new Cesium.Cartesian3.fromDegrees(0, 0);”, the p1 will already be in the “earth fixed reference frame”, with the origin at the center of the globe. When you said to “define your rectangle points in a local reference frame”, how can this be done? in particular, “You need to project the rectangle points such the origin is at the center of the rectangle”, which function in Cesium we can use for this?

Much appreciate any hints or sample code snippet.

Cheers,

Benny

6

Hi Benny,

Take a look at Scott’s answer in this thread, you’ll need to do some transformations with matrices to rotate in the correct reference frame.

Thanks,

Gabby